Citiraj:
Autor expozed
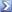
ako se pretvori taj broj u decimalni ispada:
11101110(2)=(-2)^7 + 2^6 + 2^5 + 2^3 + 2^2 + 2^1 = -128 + 110 = -18
|
Nije to dobro...

Dok pretvaras iz binarnog broja u dekadski uvijek je 2^nesto. Ne moze biti -2 nikada. Sta da smo imali zapis na 9 bitova? Tada bi ti prvi bit bio na osmu potenciju. A to je pozitivan broj...
A sad, da bi mogli reci na koji nacin ispravno oduzeti veci od manjeg binarnog broja, prvo moramo tocno definirati problem, tj. situaciju u kojoj se nalazimo (nacin na koji zapisujemo negativne binarne brojeve).
1. opcija: Negativne binarne brojeve zapisujemo isto kao i dekadske. Dakle, samo nakeljimo '-' ispred broja.
U ovom slucaju je situacija prilicno jasna. Oduzimanje cemo obaviti isto kao sto bi to napravili i s dekadskim brojevima. Okrenut cemo redoslijed brojeva i normalno oduzeti manji od vecega. Zatim ispred rezultata samo nakeljimo - i eto nam rjesenja.
No, moram reci da je ova siutacija dosta rijetka. Mozda nije neobicna negdje gdje se samo uci malo racunati s binarnim brojevima. Ali, u svijetu racunala takvo sto ne postoji.
2. opcija: Ne podrzavamo negativne binarne brojeve.
To je kao da pri deklaraciji varijable u nekom programskom jeziku (koji to podrzava) stavimo "unsigned" (samo pozitivni brojevi).
Primjer u C-u bi glasio:
unsigned int pero;
Dakle, ako koristimo 8 bita za prikaz broja, onda znaci da baratamo s brojevima iz raspona [0-255].
Ajmo to pokazati na primjeru.
Racunamo 19 - 37.
19 = 00010011
37 = 00100101
Prvo nalazimo dvojni komplement od 37.
11011010
+
00000001
---------
11011011
Sada zbrojimo 19 i dvojni komplement od 37.
00010011
+
11011011
---------
11101110 = 238
Dobili smo 238. I u ovom slucaju je to sasvim ispravan rezultat i s njime vise nista ne treba raditi. Jedino, valja primijetiti da je 238 - (255 + 1) = -18. A to je upravo onaj rezultat koji bi ocekivali u dekadskom sustavu.
3. opcija: Prvi bit koristimo kao bit predznaka.
Ako i sada koristimo 8 bitova za prikaz brojeva, onda mozemo raditi s rasponom [-128, 127] (opet je to 255 brojeva ukupno).
No, sto tocno znaci da nam prvi bit predstavlja predznak? To znaci ako je taj bit 0, onda imamo pozitivan broj, a ako je 1, onda imamo negativan broj. No, necemo tu jedinicu samo zanemariti i razmisljati o njoj kao o obicnom minusu, a o ostalih 7 bitova kao o pravom broju, nego je i ta jedinica dio broja.
Konkretno, to znaci sljedece.
Ako imamo broj kojemu je prvi bit 0, onda je to najobicniji pozitivni binarni broj i mozemo ga odmah pretvoriti u dekadski broj (na dobro poznati nacin).
No, ako je prvi bit 1, onda cemo prvo taj broj dvojno komplementirati i tek onda ga pretvoriti u dekadski broj.
Evo primjera:
(ovo je copy/paste prethodnog primjera s malo dodatka na kraju)
Racunamo 19 - 37.
19 = 00010011
37 = 00100101
Prvo nalazimo dvojni komplement od 37.
11011010
+
00000001
---------
11011011
Sada zbrojimo 19 i dvojni komplement od 37.
00010011
+
11011011
---------
11101110
Dobili smo nas rezultat, ali vidimo da je prvi bit 1, pa cemo ga dvojno komplementirati prije pretvorbe u dekadski sustav. Komplement je 00010010. A to je broj 18. Naravno, mi znamo da je on negativan, pa mozemo napisati -18.